Day 7
Today
- Computational Art kick-off
- Recursion
- Fractal drawing in Turtle World
- Optional: Loading new DNA
For Next Time
- Reading journal, Think Python 11, 12 due Monday 2/9 (but starting earlier is great)
- Project toolbox exercises have been launched. You will do at least five in total, at least three of which must be completed before spring break.
Recursion Practice
Pascal’s Triangle
Write a function called choose that takes two integer, n and k, and returns the number of ways to choose k items from a set of n (this is also known as the number of combinations of k items from a pool of n). Your solution should be implemented recursively using Pascal’s rule.
Levenshtein Distance
Write a function called levenshtein_distance that takes as input two strings
and returns the Levenshtein
distance between the two
strings. Intuitively, the Levenshtein distance is the minimum number of edit
operations to transform one string into the other (for this reason Levenshtein
distance is sometimes called “edit distance”). These edits can either be
insertions, deletions, or substitutions. Note that Levenshtein distance is
similar to Hamming distance,
but works for strings of differing lengths
Here are some examples of these operations:
- kitten → sitten (substitution of
sfork) - sitten → sittin (substitution of
ifore) - sittin → sitting (insertion of
gat the end).
While this function seems initially daunting, it admits a very compact recursive solution. You can either work on your own to see the recursive solution, or use the recursive solution given in the Wikipedia article.
We will be memoizing this function in the next reading journal to make it more computationally efficient.
Making change
Write a program that takes as input a number of cents, n, along with the denominations of some coins, d, and outputs the number of unique ways that change can be made for n cents using the coins d.
For example:
make_change(10, [1, 5, 10]) # -> 4
Specifically:
- 10 pennies
- 2 nickels
- 1 nickel 5 pennies
- 1 dime
Turtle World
Today we will explore drawing by means of attaching pens to the tails of turtles and forcing them to move around in intricate patterns. Since we’re actually quite fond of Turtles, luckily we don’t have to hurt any actual turtles but we can do this in simulation! Allen has written a wonderful package called TurtleWorld that implements this sort of drawing environment in Python (the original concept goes way back to 1967 and the Logo programming language). President Obama wrote his first line of code with a similar environment.
As part of your day 6 reading journal, you wrote several functions that operate on Turtles:
squaretakes as input the side length of a square and draws the square to the Turtle world canvaspolygontakes as input the side length and the number of sides of a regular polygoncircletakes as input the radius of a circle, which it draws by approximating a circle as a regular polygon with a large number of sidesarcextendscirclewith an extra angle parameter that controls what fraction of the circle to draw in degrees
Each of these functions is a generalization of the previous function. You also went on to draw flowers, pies, letters, spirals, or something else altogether! Thinking about how to break up large problems like these into logical smaller pieces is one of the most fun challenges in software design.
It’s often useful to think about what low-level primitive functions (such as drawing regular polygons) would be most useful in completing a task. Identifying these common primitives can help refactor messy code with many copy-paste sections into a set of reusable functions with clean interfaces. From Think Python:
The interface of a function is a summary of how it is used: what are the parameters? What does the function do? And what is the return value? An interface is “clean” if it is “as simple as possible, but not simpler. (Einstein)”
Regardless of how complex a function is to implement, its interface should be easy to understand. Well-designed functions do exactly what they say they will do without surprises.
Teleportation, Cloning, and Other Unethical Experiments on Turtles
In addition to the functions you wrote in the day 5 reading journal, there are a few other Turtle Tricks that may prove useful.
A Turtle is a Python object, which we will learn more about next week. Turtles
have methods, which we can call to inspect change their behavior. You may have
already seen one of these, the delay() function, which can be used to speed up
slowpoke Turtles.
from turtle import Turtle
speedy = Turtle()
speedy.delay(0.01)
Other important Turtle methods include xcor() and ycor)=() position, and
heading().
Read more about turtles here.
Since Turtles are simple creatures, mainly defined by their current position and heading, we can “clone” them by reading these values and using them to direct a new Turtle.
leo = Turtle()
# Create a new Turtle with the same attributes as the first
don = Turtle()
don.penup()
don.forward(leo.xcor())
don.left(90)
don.forward(leo.ycor())
don.left(leo.heading() - 90)
don.pendown()
# don.bandana_color = "purple" # TODO: Ninja functionality not yet implemented
As an exercise, encapsulate this functionality in a clone function that
takes a Turtle argument and returns a new Turtle with the same position
and heading, leaving the original Turtle untouched.
Fractals
Fractals are geometrical constructions that display self-similar repeated patterns at every scale as you zoom in. They are often extremely beautiful, and are found throughout nature. Fractals are also useful across many fields, from antenna engineering to poetry to finance. Check out Yale’s Panorama of Fractals and their Uses for more examples.
Today, we will teach our turtles to draw fractal shapes using recursion. A
very cool recursive drawing we can create is called the snowflake curve (or
Koch snowflake). To get
started, let’s write a function called snow_flake_side with the following
signature:
def snow_flake_side(turtle, length, level):
"""Draw a side of the snowflake curve with side length length and recursion
depth of level"""
The snow_flake_side function should have a base case that draws the
following image:

The recursive step should replace each of the line segments above with a
snow_flake_side with size length / 3.0 and recursion depth level - 1. Take
some time to work on this and then we’ll discuss as a group.
Once you have completed your snow_flake_side function, create a function
called snow_flake that draws the whole snowflake.
Recursive Trees
Next, we will draw a tree using recursion. Define a function called
recursive_tree that takes as input a turtle, a branch length, and a
recursion depth and draws the recursive tree to the canvas.
def recursive_tree(turtle, branch_length, level):
"""Draw a tree with branch length branch_length and recursion depth of level
"""
The base case is:

This structure is given by moving forward branch_length steps (assuming the
turtle has the correct orientation).
For the recursive step, you should:
- Draw the line as above
- Clone your turtle
- Turn the new turtle left 30 degrees
- Recurse using the cloned turtle to draw a tree with branch length
branch_length * 0.6and depth `level - 1 - Hide the cloned turtle using the
hideturtlemethod - Back the original turtle up
branch_length / 3.0 - Clone your turtle
- Turn the new turtle right 40 degrees
- Recurse using the cloned turtle to draw a tree with branch length
branch_length x 0.64and depthlevel - 1 - Hide the cloned turtle using the
hideturtlemethod
After implementing the recursive step, if you set level to 1 more than the
base case (which will either be 1 or 2 depending on what level you consider
the base case), you will get the following picture:
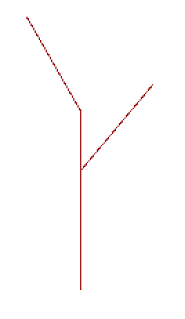
Once you’ve built your recursive_tree function, try making a few
enhancements:
- Make the base case change the pen color for the turtle to green (this will simulate the appearance of leaves if you do a high enough depth)
- Add some randomness to the degree of left turn, right turn, and scaling so that you get more naturalistic looking trees
- Add more than two branches
More Recursion
The Koch snowflake and our recursive tree are both part of a more general class of curves called L-systems (Lindenmayer Systems). Next, read the linked Wikipedia article on L-systems and try to implement Sierpinski’s triangle and fractal plant.
Hint 1: For Sierpinski’s triangle you will want to create a function to generate both symbols A and B and have them call each other.
Hint 2: For the fractal plant you should create the following functions to
save and then restore then Turtle’s state (symbols [ and ] respectively):
def save_turtle_state(turtle_states, t):
turtle_states.append((t.x, t.y, t.heading))
def restore_turtle_state(turtle_states, t):
s = turtle_states.pop()
t.x = s[0]
t.y = s[1]
t.heading = s[2]
Loading new DNA
To load the new DNA contigs for our in-class activity:
>>> from load import load_contigs
>>> contigs = load_contigs()
The variable contigs will be a list of contigs where each is encoded as a two-item tuple.
The first element of the tuple is the name of the contig, and the second element of the tuple is the DNA sequence.
To access the elements of e.g. the 5th contig, you could unpack the tuple into separate variables:
>>> name = contigs[5][0]
>>> dna_sequence = contigs[5][1]
>>> print(name)
Contig_37
Once we’ve loaded the raw DNA sequence, we still have some cleanup to do. In addition to the expected nucleotides (A, C, T, and G), the sequence includes some additional markers (K, M, S, R, W, V, and Y). These come from reading errors generated by the DNA sequencing machine. You should write a function to post-process the raw DNA sequence by replacing the additional markers with a normal nucleotide. Quick check: why not just delete the markers?
You may also want to shorten the length of your DNA sequence so that your gene finder program can run faster.
If you are finding that the output of your program is longer than the amount of text that can fit in the terminal, you can redirect the output to a file.
$ python gene_finder.py > output.txt